2024-2025学年CNAO决赛第17题-星系喷流
来自astro-init
题目
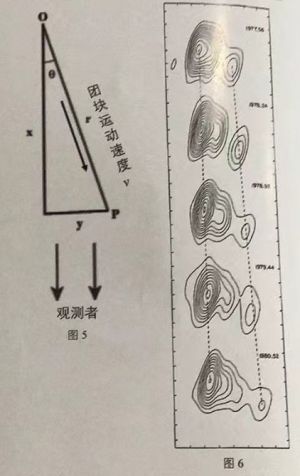
星系的高速喷流若朝着地球方向运动,则可能观测到视超光速运动(superluminalmotion)现象。如图5所示,喷流中的气体团块以速度$$v$$从$$O$$点运动到$$P$$点,运动方向与视线方向有一定夹角$$\theta$$,由于光从$$O$$点和$$P$$点到达观测者的时间有差别,导致团块横向运动(垂直于视线方向)的速度在观测者看来可能超过光速。有射电望远镜观测到一个距离为 2000Mpc 的活动星系核的喷流中的气体团块从图像上看(图6),其视横向运动角速度为-0.1毫角秒/年。假设喷流运动方向与视线方向的夹角为$$\theta=10°$$。回答时速度用光速c表示,保留两位小数。
(1)求团块的视横向速度 $$v_{\text{app}}$$
(2)记$$\beta = \frac vc, \beta_{\text{app}}=\frac{v_{\text{app}}}c$$,证明如下关系式
$$\beta=\frac{\beta_{\text{app}}}{\sin \theta + \beta_{\text{app}} \cos \theta}$$
(3)计算题中团块真实运动速度 $$v$$。
(4)由第2小问可知,$$v$$是喷流方向与视线方向的夹角$$\theta$$的函数。若我们不知道$$\theta$$的大小,那么题目中所述喷流真实速度$$v$$的最小值是多少?