2023-2024学年CNAO决赛第5题-流星测光
本页的内容需要重新排版,或者公式和图示需要重绘。请帮助完善这个页面,如果熟练的话通常不需要太多时间。 |
|
题目
流星是时标非常短的天文现象。中国科学院大学和国家天文台建设了一个流星监测网,使用广角相机拍摄流星的视频。本题给出的这颗流星是在2023年猎户座流星雨期间观测到的。表1和表2是对视频中恒星和流星的测光结果,其中列出的“流量”正比于仪器接收到的光子数。
(1)表1中列出了图4中证认出的一些恒星。请选择属于不同星座的至少5颗恒星,将恒星编号标在图4中对应恒星旁边。
(2)这颗流星是否属于猎户座流星群?
(3)大气对光线的吸收会让我们实际看到的星偏暗,星等的变化大致正比于光线穿过大气的厚度,也就是大气质量。请通过恒星测光结果拟合计算大气消光系数。
(4)使用上一问的结果,计算流星各个时刻的V波段视星等,并绘制光变曲线。
(5)(仅高年组)流星的绝对星等是指流星在100km距离处的视星等,计算流星在各个时刻的绝对星等。并估计流星体的总动能,假设流星体动能的一半可以转化为可见光。
| 编号 | 名称 | 流量 | 大气质量 | V波段星等 |
|---|---|---|---|---|
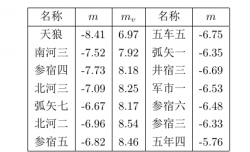
| 1 | 天狼 | 2301.5 | 1.84 | -1.44 |
| 2 | 南河三 | 1022.3 | 1.23 | 0.4 |
| 3 | 参宿四 | 1238.5 | 1.25 | 0.45 |
| 4 | 北河三 | 686.6 | 1.03 | 1.16 |
| 5 | 弧矢七 | 466.7 | 2.80 | 1.5 |
| 6 | 北河二 | 609.7 | 1.02 | 1.58 |
| 7 | 参宿五 | 533.7 | 1.32 | 1.64 |
| 8 | 五车五 | 499.3 | 1.09 | 1.65 |
| 9 | 弧矢一 | 345.4 | 2.51 | 1.83 |
| 10 | 井宿三 | 476.4 | 1.10 | 1.93 |
| 11 | 军市一 | 410.4 | 1.94 | 1.98 |
| 12 | 参宿六 | 389.4 | 1.67 | 2.07 |
| 13 | 参宿三 | 341.4 | 1.44 | 2.25 |
| 14 | 五车四 | 201.2 | 1.03 | 2.65 |
| 时间(ms) | 流量 | 大气质量 | 距离(m) |
|---|---|---|---|
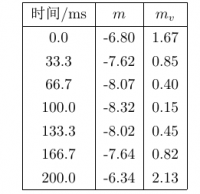
| 0.0 | 525.1 | 1.0061 | 105753 |
| 33.3 | 1112.4 | 1.0056 | 104117 |
| 66.7 | 1694.6 | 1.0053 | 102479 |
| 100.0 | 2127.2 | 1.0052 | 100910 |
| 133.3 | 1615.2 | 1.0052 | 99294ZZ |
| 166.7 | 1142.2 | 1.0054 | 97782 |
| 200.0 | 344.5 | 1.0058 | 96534 |
解析
(1)略。该图主体为冬季星空,左侧可见猎户三星。
(2)否。
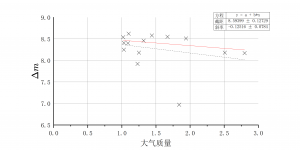
(3)计算恒星在大气外的星等需要考虑大气消光: \[ m = -2.5 \log F \] \[ m = m_v + kA + C \] 其中$$F$$为恒星的流量,$$m$$是恒星的仪器星等。恒星在大气外的星等为$$m_v$$,受到的大气消光值正比于大气质量$$A$$,其系数就是大气消光系数$$k$$。除此之外,还有常数项$$C$$。令$$\Delta m = m_v - m$$; \[ \Delta m = -kA - C \] 其中恒星的$$m$$和$$m_v$$均已知,所以$$k$$和$$C$$可由线性拟合得知。计算所有恒星的$$\Delta m$$和$$A$$,并绘制在坐标系中。
图中有两个明显偏离的点,对应天狼和南河三。最亮的两颗星的的$m$值明显偏低,说明其流量有较大的低估,可能是由部分像素过曝导致的。因此在线性拟合时将这两个点排除。拟合结果为:
\[
k = 0.1256, \quad C = -8.5952
\]
其中$$k$$即为待求的消光系数。
(4)根据上一问中的公式可以计算出流星在各个时间点的星等。
光变曲线图以时间为横轴,视星等为纵轴,注意纵轴数值向上递减,绘图应占纸面比例50%-75%,答案图略。
(5)根据星等差公式,可以得到流星的绝对星等公式: \[ M = m - 5 \log \left( \frac{r}{100 \, \text{km}} \right) \] 与太阳常数相比,可以获得流星的光度。计算流星在1au处的星等: \[ M_{\text{au}} = M - 5 \log \left( \frac{100 \, \text{km}}{1 \, \text{au}} \right) \] 与太阳光度相比: \[ M_{\text{au}} = M_{\odot} + 2.5 \log \left( \frac{L_{\text{me}}}{L_{\odot}} \right) \] 相减并整理可得: \[ M = M_{\text{au}} - 5 \log \left( \frac{100 \, \text{km}}{1 \, \text{au}} \right) + 2.5 \log \left( \frac{L_{\text{me}}}{L_{\odot}} \right) \] \[ L_{\text{me}} = 10^{\frac{M_{\odot} - M + 5 \log \left( \frac{100 \, \text{km}}{1 \, \text{au}} \right)}{2.5}} L_{\odot} \] 使用给出的流星距离计算绝对星等和光度。
| 时间/ms | M | $$L_{\text{me}}$$ / W |
|---|---|---|
| 0.0 | 1.55 | 832 |
| 33.3 | 0.77 | 1709 |
| 66.7 | 0.34 | 2522 |
| 100.0 | 0.13 | 3070 |
| 133.3 | 0.46 | 2257 |
| 166.7 | 0.87 | 1548 |
| 200.0 | 2.20 | 455 |
每帧时间0.0333秒,乘以光度并求和可得413\,J。流星体的总动能为: \[ \frac{413}{0.5} = 826 \, \text{J} \]