2019年IOAA数据分析第2题-三重掩星的等级三星系统
英文题目
2. Triply eclipsing hierarchical triple stellar system (90 p)
HD 181068 was one of the brightest targets which was continuously observed during the almost 4- year-long primary mission of NASA’s exoplanet-hunter Kepler space telescope. The spacecraft observed ≈ 3 − 4 × 10−3 magnitude dimmings every 0.453 days. (Note: The even dimmings were slightly smaller amplitude than the odd ones.) Furthermore, additional 0.007 magnitude, 2.3-day-long dimmings were detected every 22.7 days.
The correct explanation of this very unusual photometric behaviour was given by Hungarian astronomers. They found that HD 181068 is a compact hierarchical triple stellar system seen almost edge-on.
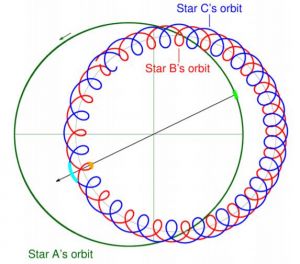
Hierarchical triple star systems consist of three stars; A, B, and C. Two of these stars (B and C) form an inner or close stellar binary system, whilst the outer component (star A) orbits at a distance from the inner system significantly larger (usually orders of magnitude) than the semi-major axis of the inner system. The schematic view of an example of a triple star system is illustrated in Fig. 2.1.
Mathematically, the motion of a hierarchical triple system can be well approximated with two
unperturbed Keplerian two-body motions; (1) Keplerian motion of the inner binary. (2) The centre of
mass of this close binary and the third star revolves on a second Keplerian orbit, “outer binary”.
In this problem, stars B and C form a P1 = 0.9056768-day-period eclipsing binary, while the centre of mass of these stars with star A forms the P2 = 45.4711-day-period outer binary. As the orbital plane of this outer orbit is seen almost edge-on from the Kepler spacecraft (and from the Earth), during their revolution on the outer orbit, stars B and C eclipse not only each other, but also star A or, a half outer revolution later are eclipsed by it, causing the extra dimmings.
i. Determination of the physical stellar sizes (and other quantities) from the geometry of the eclipses
These assumptions are used throughout this section: (1) both the inner and outer orbits are exactly circular, (2) the orbital planes of the inner and outer orbits are identical, and (3) this plane is seen exactly edge-on (i.e. 𝑖1 = 𝑖2 = 90° and 𝑖rel = 0°). Let’s consider the extra dimmings, which are central eclipses (i.e. either occultations or transits – annular eclipses), therefore, these events have four contacts. In the case of an ordinary eclipsing binary (or of a transiting exoplanet) at the times of the outer contacts the sky-projected disks of the two objects connect with each other at one point from outside, while at the inner contacts they approach each other from inside. While this last statement is also valid for outer eclipses, the situation becomes more complex, because instead of two, three stars are involved into the eclipses. However, despite this fact, we can certainly define the times of each contact from the light curve, and furthermore, we can also decide explicitly which member of the inner binary is involved in a given contact. (The other member, of course, is always star A.)
In the table below, the accurate times of some contacts of different eclipses observed by the Kepler spacecraft, the contact types and the stars are documented. Time is expressed in barycentric Julian Days (BJD).
| enent no. | contact | stars | BJD | 𝜑1 | 𝜑2 |
|---|---|---|---|---|---|
| 1 | I | A,B | 2455476.1096 | ||
| II | A,C | 2455476.4245 | |||
| III | A,B | 2455477.9677 | |||
| IV | A,B | 2455478.4722 | |||
| 2 | I | A,B | 2455521.5217 | ||
| 3 | III | A,C | 2455568.9434 | ||
| 4 | I | A,C | 2455612.4733 | ||
| III | A,C | 2455614.3571 | |||
| 5 | III | A,B | 2455659.9241 | ||
| IV | A,C | 2455660.2422 |
a) Given that 𝑇01 = 2455051.2361 and 𝑇02 = 2455522.7318 denote the time of an inferior conjunction of the inner and outer binaries respectively (i.e. that time, when, from the perspective of the observer, star C eclipses star B, and when star A eclipses the centre of mass of stars B and C.)
Define
𝜑1 (𝑡) = {(𝑡 − 𝑇01)⁄𝑃1 }, and 𝜑2 (𝑡) = {(𝑡 − 𝑇02)⁄𝑃2 }
as the photometric phases of the inner and outer binaries respectively. {𝑥} denotes the decimal part of the real number 𝑥. If {𝑥} < 0, use {𝑥} + 1 instead. Calculate the phases for the times of the tabulated contact events and write the answers in the appropriatecolumns of the table on the answer sheet Round your answers to four decimal places. (10 p)
b) Determine, whether star A, or the close binary (i.e. stars B and C) were closer to the observer during each eclipsing event. Write your answer in the table on the answer sheet.(5 p)
c) Using the table above, calculate (1) the dimensionless radius of each star relative to the semi-major axis of the outer orbit (𝑅A,B,C⁄𝑎2), (2) the ratio of the semi-major axes of the two orbits (𝑎1⁄𝑎2) and (3) the mass ratio of stars B and C (𝑞1 = 𝑚C⁄𝑚B). Hint: Use at least four decimal place accuracy in your calculations. Be cautious, it may not be possible to use all theoretically possible contact combinations with a given limited accuracy of time data. (30 p)
d) Based on the results obtained above, calculate the outer mass ratio (𝑞2 = 𝑚BC⁄𝑚A). (8 p)
ii. Dynamical determination of the stellar masses using radial velocity (RV) and eclipse timing variations (ETV) measurements
To obtain RV data, ground-based spectroscopic follow up observations were carried out with four different instruments. Only the lines of star A were detectable in all spectra. Plotting all the measurements against time, the RV curve was nicely fitted in the following form:
𝑉rad,A = 𝑉𝛾 + 𝐾A sin𝜙RV
where 𝑉𝛾 is the systemic velocity and 𝐾𝐴 is the velocity amplitude:
𝑉𝛾 = 6.993 ± 0.011 km s−1 , 𝐾A = 37.195 ± 0.053 km s−1 ,
𝑃2 = 45.4711 ± 0.0002 d, 𝜙RV = $$\frac{2\pi}{P_2}$$ [𝑡 − (2455522.7318 ± 0.0095)].
Furthermore, the researchers determined the mid-times of the regular eclipses of the close binary (formed by stars B and C), and found that the occurrence of for example the eclipsing minima belonging to the N th orbital revolution can be described by the simple expression:
𝑇𝑁 = 𝑇0 + 𝑃1𝑁 + 𝐴ETV sin ( $$\frac{2\pi}{P_2}$$ 𝑃1𝑁 + 𝜙0),
where
𝑇0 = BJD 2455051.23607 ± 5 × 10−5 , 𝑃1 = 0.9056768 ± 3 × 10−7 d,
𝐴ETV = 0.001446 ± 0.000110 d, 𝜙0 = −0.76779 ± 0.01937 rad.
In this expression AETV is the amplitude of the eclipse timing variation, 𝑇0 denotes the mid-eclipse time of the reference (zeroth) primary eclipse, and N is the cycle number, which is an integer for primary eclipses (i.e. when the slightly fainter star C eclipses star B), and half-integer for secondary ones (i.e. when star B eclipses star C).
Determine (1) again the mass ratio (𝑞2 = 𝑚BC⁄𝑚A) of the centre of mass of the inner binary and star A using only the results obtained in point ii., (2) the mass of component A (𝑚A ) and (3) the total mass of the inner, close binary (𝑚BC). Calculate the errors for (1), (2), and (3) in masses. Hint: You can save much time by expressing the masses in solar mass and the orbital separations either in solar radius or au.(22 p)
iii. Using results obtained in questions 1 and 2, determine the masses of stars B and C respectively and calculate the physical dimensions of all three stars (i.e. stellar radii in physical units). (15 p)