“2019年BAAO第1题-帕克太阳探测器”的版本间的差异
(→英文解答) |
(→英文解答) |
||
| 第106行: | 第106行: | ||
'''cx''' = '''cz''' = ''a'' | '''cx''' = '''cz''' = ''a'' | ||
| + | |||
| + | '''SP''' = ''r'' | ||
| + | |||
| + | '''cS''' = ''ae'' | ||
| + | |||
| + | '''cd''' = ''U'' | ||
| + | |||
| + | '''Pd''' = ''V'' | ||
| + | |||
| + | therefore '''Sd''' = '''cd''' – '''cs''' = ''U'' – ''ae'' | ||
| + | |||
| + | For an ellipse, the general equation is $$\frac{U^2}{a^2}+\frac{V^2}{b^2}=1$$, so the points (U,V) on the ellipse are | ||
| + | |||
| + | $$cos\ E=\frac{U}{a}$$ and $$sin\ E=\frac{V}{b}$$ [''1 mks''] | ||
| + | |||
| + | We are also given that $$e=\sqrt{1-\frac{b^2}{a^2}}\ \therefore\ b^2=a^2(1-e^2)$$ | ||
==中文题目== | ==中文题目== | ||
==中文解答== | ==中文解答== | ||
2019年10月7日 (一) 20:00的版本
英文题目
Qu 1. Parker Solar Probe
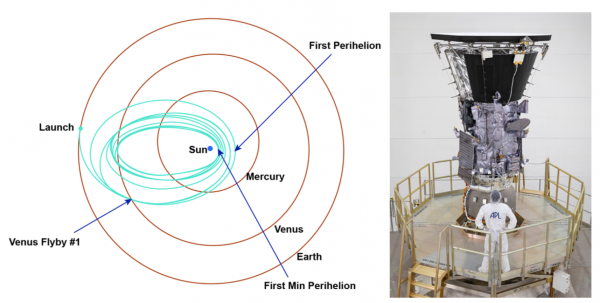
The Parker Solar Probe (PSP) is part of a mission to learn more about the Sun, named after the scientist that first proposed the existence of the solar wind, and was launched on 12th August 2018. Over the course of the 7 year mission it will orbit the Sun 24 times, and through 7 flybys of Venus it will lose some energy in order to get into an ever tighter orbit (see Figure 1). In its final 3 orbits it will have a perihelion (closest approach to the Sun) of only $$r_{peri} = 9.86 R_{⊙}$$, about 7 times closer than any previous probe, the first of which is due on 24th December 2024. In this extreme environment the probe will not only face extreme brightness and temperatures but also will break the record for the fastest ever spacecraft.
Figure 1: Left: The journey PSP will take to get from the Earth to the final orbit around the Sun. Right: The probe just after assembly in the John Hopkins University Applied Physics Laboratory. Credit: NASA / John Hopkins APL / Ed Whitman.
a. When the probe is at its closest perihelion:
(i) Calculate the apparent magnitude of the Sun, given that from Earth $$m_{⊙} = −26.74$$.
(ii) Calculate the temperature the heat shield must be able to survive. Assume that the heat shield of the probe absorbs all of the incident radiation, radiates as a perfect black body, and that only one side of the probe ever faces the Sun (to protect the instruments) such that the emitting (surface) area is double the absorbing (cross-sectional) area.
b. The speed, $$v$$, of an object in an elliptical orbit of semi-major axis $$a$$ around an object of mass $$M$$ when a distance $$r$$ away can be calculated as
$$v^2=GM(\frac{2}{r}-\frac{1}{a})$$.
Given that in its final orbit PSP has a orbital period of 88 days, calculate the speed of the probe as it passes through the minimum perihelion. Give your answer in km s−1.
c. After the first flyby of Venus on 3rd October 2018 it was moved into an orbit with a 150 day period, and the subsequent first perihelion on 6th November 2018 was at a distance of 35.7 $$R_⊙$$. Given its mass at launch was 685 kg, calculate the total amount of energy that had to be lost by the probe to get from this first orbit (ignoring the orbital properties prior to the Venus flyby) to the final orbit. Ignore any change in the mass of the probe due to burning fuel.
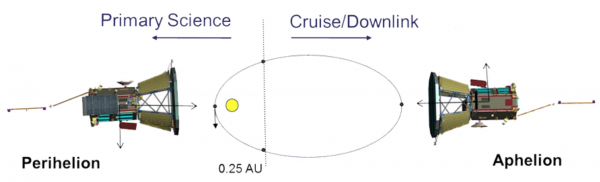
Close to the Sun the communications equipment is very sensitive to the extreme environment, so the mission is planned for the probe to take all of its primary science measurements whilst within 0.25 au of the Sun, and then to spend the rest of the orbit beaming that data back to Earth, as shown in Figure 2.
Figure 2: The way PSP is planned to split each orbit into taking measurements and sending data back. Credit: NASA / Johns Hopkins APL.
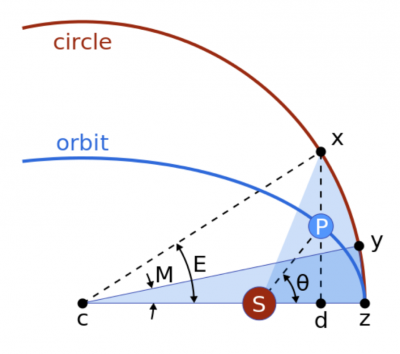
When considering the position of an object in an elliptical orbit as a function of time, there are two important angles (called ‘anomalies’) necessary to do the calculation, and they are defined in Figure 3. By constructing a circular orbit centred on the same point as the ellipse and with the same orbital period, the eccentric anomaly, E, is then the angle between the major axis and the perpendicular projection of the object (some time t after perihelion) onto the circle as measured from the centre of the ellipse (∠xcz in the figure). The mean anomaly, M, is the angle between the major axis and where the object would have been at time t if it was indeed on the circular orbit (∠ycz in the figure, such that the shaded areas are the same).
Figure 3: The definitions of the anomalies needed to get the position of an object in an ellipse as a function of time. The Sun (located at the focus) is labeled S and the probe P . M and E are the mean and eccentric anomalies respectively. The angle θ is called the true anomaly and is not needed for this question. Credit: Wikipedia.
d. Derive a formula for the distance from the focus for an elliptical orbit, r (SP in the figure) in terms of the semi-major axis a, the eccentricity e, and the eccentric anomaly E.
The eccentric anomaly can be related to the mean anomaly through Kepler’s Equation,
M = E − e sin E .
e. Calculate how long PSP spends doing primary science in its final orbit. Give your answer in days.
英文解答
Q1 - Parker Solar Probe [25 marks]
a. (i) [2 mks] ratio of brightness, $$\frac{b_1}{b_0} = \frac{(1\rm\ au)^2}{9(.86\rm\ R_{\odot})^2}=\frac{(1.50\times10^{11})^2}{(9.86\times6.96\times10^8)^2}=478$$ [1 mks]
$$\therefore m_{new}=m_{\odot}-2.5\rm log(\frac{b_1}{b_0})=-26.74-6.698=-33.44$$ [1 mks]
[Allow calculating the solar absolute magnitude, $$M_{\odot}=4.29$$, as an alternative first mark]
a. (ii) [3 mks] For thermal balance, power absorbed must equal power emitted, so
$$\frac{L_{odot}}{4\pi r^2}\times A_{abs}=\sigma A_{emit}T^4$$
But since $$A_{emit}=2\times A_{abs}$$ then
$$\frac{L_{odot}}{4\pi r^2}=2\sigma T^4$$
$$\therefore T=\sqrt[4]{\frac{L_{odot}}{8\pi \sigma r^2}}$$ [1 mks]
$$T=\sqrt[4]{\frac{3.85\times10^{26}}{8\pi \times 5.67\times10^{-8}\times (9.86\times6.96\times10^8)^2}}$$ [1 mks]
$$T=1550\rm\ K$$ [1 mks]
b. [4 mks] Using Kepler’s third law to find the semi-major axis of the final orbit,
$$T^2=\frac{4\pi^2}{GM}a^3$$
$$\therefore a=\sqrt[3]{\frac{GM}{4\pi^2}T^2}=\sqrt[3]{\frac{6.67\times10^{-11}\times1.99\times10^{30}}{4\pi^2}\times(88\times24\times3600)^2} $$ [1 mks]
$$a=5.79\times 10^{10}\rm \ m$$ [1 mks]
$$v=\sqrt{GM(\frac{2}{r}-\frac{1}{a})}=\sqrt{6.67\times10^{-11}\times1.99\times10^{30}(\frac{2}{9.86\times6.96\times10^8}-\frac{1}{5.79\times10^{10}})}$$ [1 mks]
$$v=(190776\rm \ m\ s^{-1})=191\rm km\ s^{-1}$$ [Must be in km s-1] [1 mks]
[This will mean that the Parker Solar Probe will become the fastest spacecraft (relative to the Sun) ever flown – at this speed you could travel from New York to Tokyo in less than a minute!]
c. [7 mks] Using a similar method to the previous question to work out the semi-major axis and perihelion speed for the first orbit,
$$a_{initial}=8.27\times10^{10}\rm \ m$$ [1 mks]
$$v_{initial}=95.3\rm \ km\ s^{-1}$$ [1 mks]
The total energy is the sum of the potential and kinetic energies,
$$E_{tot}=E_p+E_k$$ and $$E_p=-\frac{GM}{r}$$
At the first perihelion,
$$E_{tot}=-\frac{6.67\times10^{-11}\times1.99\times10^{30}\times685}{35.7\times6.96\times10^8}+\frac{1}{2}\times685\times(95279)^2$$ $$E_{tot}=-3.66\times10^{12}+3.11\times10^{12}=-5.50\times10^{11}\rm\ J$$ [Allow 1 mark if only have a correct Ep or Ek term] [2 mks]
At the final perihelion,
$$E_{tot}=-\frac{6.67\times10^{-11}\times1.99\times10^{30}\times685}{9.86\times6.96\times10^8}+\frac{1}{2}\times685\times(190766)^2$$ $$E_{tot}=-1.32\times10^{13}+1.25\times10^{13}=-7.85\times10^{11}\rm\ J$$ [Allow 1 mark if only have a correct Ep or Ek term] [2 mks]
$$\therefore \Delta E_{tot}=2.35\times10^{11}\rm\ J$$ [Ignore a minus sign] [1 mks]
d. [4 mks] In Figure 3,
cx = cz = a
SP = r
cS = ae
cd = U
Pd = V
therefore Sd = cd – cs = U – ae
For an ellipse, the general equation is $$\frac{U^2}{a^2}+\frac{V^2}{b^2}=1$$, so the points (U,V) on the ellipse are
$$cos\ E=\frac{U}{a}$$ and $$sin\ E=\frac{V}{b}$$ [1 mks]
We are also given that $$e=\sqrt{1-\frac{b^2}{a^2}}\ \therefore\ b^2=a^2(1-e^2)$$