2019年BAAO第1题-帕克太阳探测器
本页内容不完整。如果你掌握本页面空缺的相关信息,请帮助完善这个页面。 |
|
英文题目
Qu 1. Parker Solar Probe
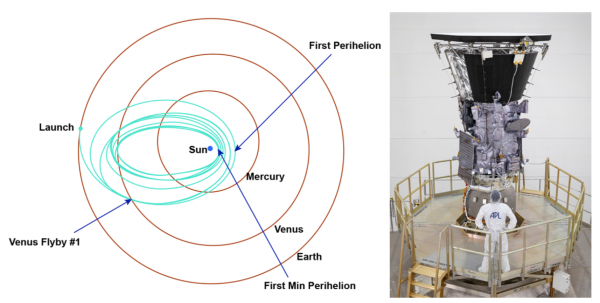
The Parker Solar Probe (PSP) is part of a mission to learn more about the Sun, named after the scientist that first proposed the existence of the solar wind, and was launched on 12th August 2018. Over the course of the 7 year mission it will orbit the Sun 24 times, and through 7 flybys of Venus it will lose some energy in order to get into an ever tighter orbit (see Figure 1). In its final 3 orbits it will have a perihelion (closest approach to the Sun) of only $$r_{peri} = 9.86 R_{⊙}$$, about 7 times closer than any previous probe, the first of which is due on 24th December 2024. In this extreme environment the probe will not only face extreme brightness and temperatures but also will break the record for the fastest ever spacecraft.
Figure 1: Left: The journey PSP will take to get from the Earth to the final orbit around the Sun. Right: The probe just after assembly in the John Hopkins University Applied Physics Laboratory. Credit: NASA / John Hopkins APL / Ed Whitman.
a. When the probe is at its closest perihelion:
(i) Calculate the apparent magnitude of the Sun, given that from Earth $$m_{⊙} = −26.74$$.
(ii) Calculate the temperature the heat shield must be able to survive. Assume that the heat shield of the probe absorbs all of the incident radiation, radiates as a perfect black body, and that only one side of the probe ever faces the Sun (to protect the instruments) such that the emitting (surface) area is double the absorbing (cross-sectional) area.
b. The speed, $$v$$, of an object in an elliptical orbit of semi-major axis $$a$$ around an object of mass $$M$$ when a distance $$r$$ away can be calculated as
$$v^2=GM(\frac{2}{r}-\frac{1}{a})$$.
Given that in its final orbit PSP has a orbital period of 88 days, calculate the speed of the probe as it passes through the minimum perihelion. Give your answer in km s−1.
c. After the first flyby of Venus on 3rd October 2018 it was moved into an orbit with a 150 day period, and the subsequent first perihelion on 6th November 2018 was at a distance of 35.7 $$R_⊙$$. Given its mass at launch was 685 kg, calculate the total amount of energy that had to be lost by the probe to get from this first orbit (ignoring the orbital properties prior to the Venus flyby) to the final orbit. Ignore any change in the mass of the probe due to burning fuel.
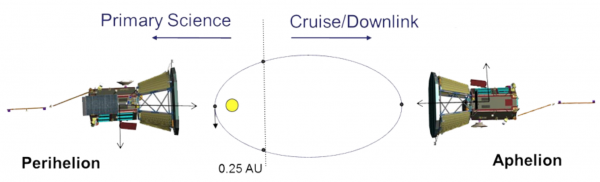
Close to the Sun the communications equipment is very sensitive to the extreme environment, so the mission is planned for the probe to take all of its primary science measurements whilst within 0.25 au of the Sun, and then to spend the rest of the orbit beaming that data back to Earth, as shown in Figure 2.
Figure 2: The way PSP is planned to split each orbit into taking measurements and sending data back. Credit: NASA / Johns Hopkins APL.
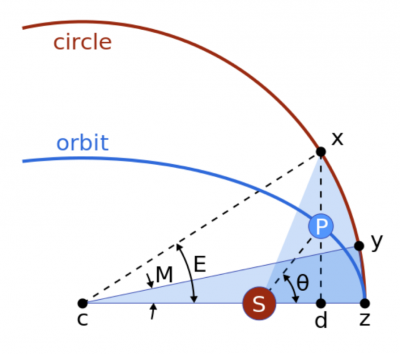
When considering the position of an object in an elliptical orbit as a function of time, there are two important angles (called ‘anomalies’) necessary to do the calculation, and they are defined in Figure 3. By constructing a circular orbit centred on the same point as the ellipse and with the same orbital period, the eccentric anomaly, E, is then the angle between the major axis and the perpendicular projection of the object (some time t after perihelion) onto the circle as measured from the centre of the ellipse (∠xcz in the figure). The mean anomaly, M, is the angle between the major axis and where the object would have been at time t if it was indeed on the circular orbit (∠ycz in the figure, such that the shaded areas are the same).
Figure 3: The definitions of the anomalies needed to get the position of an object in an ellipse as a function of time. The Sun (located at the focus) is labeled S and the probe P . M and E are the mean and eccentric anomalies respectively. The angle θ is called the true anomaly and is not needed for this question. Credit: Wikipedia.
d. Derive a formula for the distance from the focus for an elliptical orbit, r (SP in the figure) in terms of the semi-major axis a, the eccentricity e, and the eccentric anomaly E.
The eccentric anomaly can be related to the mean anomaly through Kepler’s Equation,
M = E − e sin E .
e. Calculate how long PSP spends doing primary science in its final orbit. Give your answer in days.
英文解答
Q1 - Parker Solar Probe [25 marks]
a. (i) [2 mks] ratio of brightness, $$\frac{b_1}{b_0} = \frac{(1\rm\ au)^2}{9(.86\rm\ R_{\odot})^2}=\frac{(1.50\times10^{11})^2}{(9.86\times6.96\times10^8)^2}=478$$ [1 mks]
$$\therefore m_{new}=m_{\odot}-2.5\rm log(\frac{b_1}{b_0})=-26.74-6.698=-33.44$$ [1 mks]
[Allow calculating the solar absolute magnitude, $$M_{\odot}=4.29$$, as an alternative first mark]
a. (ii) [3 mks] For thermal balance, power absorbed must equal power emitted, so
$$\frac{L_{odot}}{4\pi r^2}\times A_{abs}=\sigma A_{emit}T^4$$
But since $$A_{emit}=2\times A_{abs}$$ then
$$\frac{L_{odot}}{4\pi r^2}=2\sigma T^4$$
$$\therefore T=\sqrt[4]{\frac{L_{odot}}{8\pi \sigma r^2}}$$ [1 mks]
$$T=\sqrt[4]{\frac{3.85\times10^{26}}{8\pi \times 5.67\times10^{-8}\times (9.86\times6.96\times10^8)^2}}$$ [1 mks]
$$T=1550\rm\ K$$ [1 mks]
b. [4 mks] Using Kepler’s third law to find the semi-major axis of the final orbit,
$$T^2=\frac{4\pi^2}{GM}a^3$$
$$\therefore a=\sqrt[3]{\frac{GM}{4\pi^2}T^2}=\sqrt[3]{\frac{6.67\times10^{-11}\times1.99\times10^{30}}{4\pi^2}\times(88\times24\times3600)^2} $$ [1 mks]
$$a=5.79\times 10^{10}\rm \ m$$ [1 mks]
$$v=\sqrt{GM(\frac{2}{r}-\frac{1}{a})}=\sqrt{6.67\times10^{-11}\times1.99\times10^{30}(\frac{2}{9.86\times6.96\times10^8}-\frac{1}{5.79\times10^{10}})}$$ [1 mks]
$$v=(190776\rm \ m\ s^{-1})=191\rm km\ s^{-1}$$ [Must be in km s-1] [1 mks]
[This will mean that the Parker Solar Probe will become the fastest spacecraft (relative to the Sun) ever flown – at this speed you could travel from New York to Tokyo in less than a minute!]
c. [7 mks] Using a similar method to the previous question to work out the semi-major axis and perihelion speed for the first orbit,
$$a_{initial}=8.27\times10^{10}\rm \ m$$ [1 mks]
$$v_{initial}=95.3\rm \ km\ s^{-1}$$ [1 mks]
The total energy is the sum of the potential and kinetic energies,
$$E_{tot}=E_p+E_k$$ and $$E_p=-\frac{GM}{r}$$
At the first perihelion,
$$E_{tot}=-\frac{6.67\times10^{-11}\times1.99\times10^{30}\times685}{35.7\times6.96\times10^8}+\frac{1}{2}\times685\times(95279)^2$$
$$E_{tot}=-3.66\times10^{12}+3.11\times10^{12}=-5.50\times10^{11}\rm\ J$$ [Allow 1 mark if only have a correct Ep or Ek term] [2 mks]
At the final perihelion,
$$E_{tot}=-\frac{6.67\times10^{-11}\times1.99\times10^{30}\times685}{9.86\times6.96\times10^8}+\frac{1}{2}\times685\times(190766)^2$$
$$E_{tot}=-1.32\times10^{13}+1.25\times10^{13}=-7.85\times10^{11}\rm\ J$$ [Allow 1 mark if only have a correct Ep or Ek term] [2 mks]
$$\therefore \Delta E_{tot}=2.35\times10^{11}\rm\ J$$ [Ignore a minus sign] [1 mks]
d. [4 mks] In Figure 3,
cx = cz = a
SP = r
cS = ae
cd = U
Pd = V
therefore Sd = cd – cs = U – ae
For an ellipse, the general equation is $$\frac{U^2}{a^2}+\frac{V^2}{b^2}=1$$, so the points (U,V) on the ellipse are
$$cos\ E=\frac{U}{a}$$ and $$sin\ E=\frac{V}{b}$$ [1 mks]
We are also given that $$e=\sqrt{1-\frac{b^2}{a^2}}\ \therefore\ b^2=a^2(1-e^2)$$
Using Pythagoras' theorem,
(SP)2=(Pd)2+(Sd)2
$$\therefore\ r^2=(b\ sin\ E)^2+(a\ cos\ E-ae)^2$$ [1 mks]
$$ r^2=a^2(1-e^2)\times(1-cos^2\ E)+a^2(cos^2\ E-2e\ cos\ E+e^2)$$ [1 mks]
$$r^2=a^2-2a^2e\ cos\ E+a^2e^2\ cos^2\ E=a^2(1-e\ cos\ E)^2$$
$$\therefore\ r=a(1-e\ cos\ E)$$ [1 mks]
[Third mark is for eliminating b and writing all expressions in terms of only one trigonometric function. A reasonable attempt at a derivation (allowing alternative methods) must be present to get the marks for this question (simply writing the answer only scores 1 mark)]
e. [5 mks] With the perihelion distance we can find the eccentricity,
$$r_{peri}=a(1-e)\therefore\ e=1-\frac{r_{peri}}{a}=1-\frac{9.86\times6.96\times10^8}{5.79\times10^{10}}=0.882$$ [1 mks]
Using the formula just derived we can find E for r = 0.25 au,
$$E=cos^{-1}(\frac{1}{e}(1-\frac{r}{a}))=cos^{-1}(\frac{1}{0.882}(1-\frac{0.25\times1.50\times10^{11}}{5.79\times10^{10}}))=1.16\rm\ rad(=66.4^{\circ})$$ [1 mks]
Using the formula given we can find M,
$$M=E-e\ sin\ E=1.16-0.882\times sin\ 1.16=0.351\rm\ rad(=20.1^{\circ})$$ [1 mks]
Allowing for both sides of the ellipse, $$\Delta M=0.703\rm\ rad(=40.3^{\circ})$$ [1 mks]
Movement through the circular orbit has constant angular velocity, meaning
$$\frac{\Delta M}{\Delta t}=\frac{2\pi}{T}\ \therefore\ \Delta t=\frac{T\Delta M}{2\pi}=\frac{88\times0.703}{2\pi}=9.84\rm\ days(=9\ days\ 20\ hours\ 12\ mins)$$ [1 mks]
[If they forget the factor of two (so $$\Delta t = 4.92\rm\ days$$) allow 4 marks. Allow ±1 hour on the final answer to account for intermediate rounding errors. Allow full ecf for using their value of the semi-major axis from part b. Must be given in days for the final mark]
中文题目
Qu 1. 帕克太阳探测器
帕克太阳探测器(PSP)是太阳深入研究任务的一部分,以最早发现太阳风存在的科学家命名,于2018年8月12日发射,在为期7年的飞行过程中,它将绕太阳运行24圈。通过七次飞临金星,它会失去一些能量,从而进入更半长轴更小的轨道(见图一)。在最后运行的三个轨道周期,它的近日点(最接近太阳)只有 $$r_{peri} = 9.86 R_{⊙}$$,比以往探测器都更近7倍,在这种极端环境下,探测器不仅将面临极端的光照和温度,而且还将打破有史以来最快的航天器的记录。
图一:左图:PSP将从地球到达太阳的最后轨道。右图:探测器刚在约翰霍普金斯大学应用物理实验室组装完毕。图源:美国宇航局/约翰·霍普金斯大学应用物理实验室/埃德·惠特曼(NASA / John Hopkins APL / Ed Whitman.)。
a.当探测器处于最近的近日点时:
(i) 计算在该点的太阳视星等,在地球上的太阳视星等$$m_{⊙} = −26.74$$。
(ii) 计算隔热层的需要达到的最小耐热温度。假设探测器的热屏蔽吸收了所有入射辐射、且为完美黑体,同时探测器只有一面面向太阳(为了保护仪器)使得辐射发散面积(表面)是吸收面积(横截面)的两倍。
b.已知轨道半长轴为$$a$$ ,中心天体质量为$$M$$,当距离为 $$r$$,速度$$v$$可表示为
$$v^2=GM(\frac{2}{r}-\frac{1}{a})$$.
已知在最后的轨道上探测器绕行周期为88天,计算探测器在近日点的速度,答案单位为km s−1。‘
c.在2018年10月3日,第一次飞临金星之后,探测器转移至周期为150天的轨道,在随后的8018年11月6日第一次到达近日点距离太阳35.7 $$R_⊙$$。已知发射时质量为685kg,计算探测器从第一个轨道(忽略金星飞越之前的轨道特性)到最终轨道所损失的总能量。忽略探测器质量因燃烧燃料而发生的任何变化。
在靠近太阳的地方,通讯设备对极端环境非常敏感。所以这次任务是计划让探测器在离太阳0.25AU的范围内进行所有的主要科学探测,然后在轨道其他部分时把数据发回地球,见图二。
图二:PSP计划将每个轨道分成测量和发回数据的方式。图源:NASA / Johns Hopkins APL。
当考虑物体在椭圆轨道上的位置随时间变化,有两个重要的角度(称为’anomalies‘)需要计算,如图三所示。通过构造以椭圆为中心、轨道周期相同的圆轨道,偏心 anomalies E,是指物体的主轴与垂直投影之间的夹角(近日点后一段时间 t)从椭圆中心测量到圆上(图中为∠xcz)。平均anomalies,M,是长轴之间的夹角,如果物体确实在圆形轨道上,那么它在时间t上(图中是∠ycz,因此阴影区域是相同的)
图三:作为时间函数得到物体在椭圆中的位置所需的异常的定义。太阳(位于焦点处)被标记为S和探针P。M和E分别是平均anomalies和偏心anomalies。角度θ被称为真anomalies,这个问题不需要考虑。图源:维基百科。
d.导出了椭圆轨道焦距r(图中SP)的半长轴a、偏心率e和偏心异常E的计算公式。
偏心异常可通过开普勒方程M=E−e sin E与平均anomalies有关,
M = E − e sin E 。
e.计算PSP在其最终轨道上做初级科学的时间。答案以天为单位。
中文解答
Q1 - 帕克太阳探测器 [25 分]
a. (i) [2 mks] 亮度比, $$\frac{b_1}{b_0} = \frac{(1\rm\ au)^2}{9(.86\rm\ R_{\odot})^2}=\frac{(1.50\times10^{11})^2}{(9.86\times6.96\times10^8)^2}=478$$ [1 分]
$$\therefore m_{new}=m_{\odot}-2.5\rm log(\frac{b_1}{b_0})=-26.74-6.698=-33.44$$ [1 分]
[允许以太阳绝对星等计算, $$M_{\odot}=4.29$$]
a. (ii) [3 mks] 为了热平衡,能量吸收率必须等于能量散发率, 所以
$$\frac{L_{odot}}{4\pi r^2}\times A_{abs}=\sigma A_{emit}T^4$$
But since $$A_{emit}=2\times A_{abs}$$ then
$$\frac{L_{odot}}{4\pi r^2}=2\sigma T^4$$
$$\therefore T=\sqrt[4]{\frac{L_{odot}}{8\pi \sigma r^2}}$$ [1 分]
$$T=\sqrt[4]{\frac{3.85\times10^{26}}{8\pi \times 5.67\times10^{-8}\times (9.86\times6.96\times10^8)^2}}$$ [1 分]
$$T=1550\rm\ K$$ [1分]
b. [4分] 利用开普勒第三定律求出最终轨道的半长轴,
$$T^2=\frac{4\pi^2}{GM}a^3$$
$$\therefore a=\sqrt[3]{\frac{GM}{4\pi^2}T^2}=\sqrt[3]{\frac{6.67\times10^{-11}\times1.99\times10^{30}}{4\pi^2}\times(88\times24\times3600)^2} $$ [1分]
$$a=5.79\times 10^{10}\rm \ m$$ [1分]
$$v=\sqrt{GM(\frac{2}{r}-\frac{1}{a})}=\sqrt{6.67\times10^{-11}\times1.99\times10^{30}(\frac{2}{9.86\times6.96\times10^8}-\frac{1}{5.79\times10^{10}})}$$ [1分]
$$v=(190776\rm \ m\ s^{-1})=191\rm km\ s^{-1}$$ [Must be in km s-1] [1分]
[这意味着帕克太阳探测器会变成史上最快的航天器(相对与太阳),这个速度相当于我们可以在一分钟内从纽约到东京]
c. [7分] 用与前面问题类似的方法计算出第一轨道的半长轴和近日点速度。,
$$a_{initial}=8.27\times10^{10}\rm \ m$$ [1 mks]
$$v_{initial}=95.3\rm \ km\ s^{-1}$$ [1 mks]
总能量是势能和动能之和,
$$E_{tot}=E_p+E_k$$ and $$E_p=-\frac{GM}{r}$$
在第一个近日点,
$$E_{tot}=-\frac{6.67\times10^{-11}\times1.99\times10^{30}\times685}{35.7\times6.96\times10^8}+\frac{1}{2}\times685\times(95279)^2$$
$$E_{tot}=-3.66\times10^{12}+3.11\times10^{12}=-5.50\times10^{11}\rm\ J$$ [如果Ep 或 Ek只有一个正确的,得1分。] [2分]
在最后一个近日点,
$$E_{tot}=-\frac{6.67\times10^{-11}\times1.99\times10^{30}\times685}{9.86\times6.96\times10^8}+\frac{1}{2}\times685\times(190766)^2$$
$$E_{tot}=-1.32\times10^{13}+1.25\times10^{13}=-7.85\times10^{11}\rm\ J$$ [Allow 1 mark if only have a correct Ep or Ek term] [2 mks]
$$\therefore \Delta E_{tot}=2.35\times10^{11}\rm\ J$$ [忽略负号] [1分]
d. [4分] 在图三,
cx = cz = a
SP = r
cS = ae
cd = U
Pd = V
所以 Sd = cd – cs = U – ae
对于椭圆,一般方程是 $$\frac{U^2}{a^2}+\frac{V^2}{b^2}=1$$, 椭圆上的点(U,V)是$$cos\ E=\frac{U}{a}$$ and $$sin\ E=\frac{V}{b}$$ [1 mks]
同时 $$e=\sqrt{1-\frac{b^2}{a^2}}\ \therefore\ b^2=a^2(1-e^2)$$
由毕格拉斯定理,
(SP)2=(Pd)2+(Sd)2
$$\therefore\ r^2=(b\ sin\ E)^2+(a\ cos\ E-ae)^2$$ [1分]
$$ r^2=a^2(1-e^2)\times(1-cos^2\ E)+a^2(cos^2\ E-2e\ cos\ E+e^2)$$ [1分]
$$r^2=a^2-2a^2e\ cos\ E+a^2e^2\ cos^2\ E=a^2(1-e\ cos\ E)^2$$
$$\therefore\ r=a(1-e\ cos\ E)$$ [1分]
[3分是消除b和写所有的表达式,只有一个三角函数。为了得到这个问题的分数,必须有一个合理的推导尝试(允许选择其他方法)(只写出答案,分数只有1分)。]
e. [5分] 有了近日点距离,我们就能找到偏心点,
$$r_{peri}=a(1-e)\therefore\ e=1-\frac{r_{peri}}{a}=1-\frac{9.86\times6.96\times10^8}{5.79\times10^{10}}=0.882$$ [1分]
利用刚刚导出的公式,我们可以找到 E对于r = 0.25 au,
$$E=cos^{-1}(\frac{1}{e}(1-\frac{r}{a}))=cos^{-1}(\frac{1}{0.882}(1-\frac{0.25\times1.50\times10^{11}}{5.79\times10^{10}}))=1.16\rm\ rad(=66.4^{\circ})$$ [1分]
利用公式我们可得 M,
$$M=E-e\ sin\ E=1.16-0.882\times sin\ 1.16=0.351\rm\ rad(=20.1^{\circ})$$ [1分]
Allowing for both sides of the ellipse, $$\Delta M=0.703\rm\ rad(=40.3^{\circ})$$ [1 分]
通过圆形轨道的运动具有恒定的角速度,则
$$\frac{\Delta M}{\Delta t}=\frac{2\pi}{T}\ \therefore\ \Delta t=\frac{T\Delta M}{2\pi}=\frac{88\times0.703}{2\pi}=9.84\rm\ days(=9\ days\ 20\ hours\ 12\ mins)$$ [1 分]
[如果未给出2的因子(所以Δt=4.92天,Δt=4.92天),那么得4分。在最终答案上允许±1小时计算中间舍入误差。允许使用来自b部的半长轴的所有椭圆曲线分解(ecf)。答案必须以天为单位给出,否则扣1分]