2024年IOAA理论第2题-星系团

	由ai生成 本页内容由ai生成。请帮助校对和完善这个页面。

英文题目

T2. Galaxy Cluster (10 points)

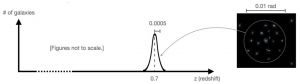
An astrophysical survey mapped all the galaxies in a small region of the sky, of angular diameter \(\Delta\theta=0.01\) rad, where many galaxies seemed to be concentrated around the central area of the image. When the positions and redshifts of all the galaxies in this cluster were measured, an interesting distribution emerged, which is shown in the plot below.

图一 星系红移分布

Using these observations, estimate the total mass of the galaxy cluster and express your answer in solar masses. Assume that this galaxy cluster is in dynamical equilibrium, with a root-mean-square redshift dispersion \(\sigma_{z}=\sqrt{\langle(z-0.7)^{2}\rangle}=0.0005\). Feel free to make reasonable approximations when considering the average velocities, masses, and spatial distribution of the galaxies.

Consider that the distance to \(\bar{z}=0.7\) in the standard cosmological model is \(D_{A}=1500\) Mpc. Ignore cosmological effects on the distance.

中文翻译

T2. 星系团（10分）

一项天体物理巡天项目绘制了天空中角直径\(\Delta\theta=0.01\)弧度的小区域内所有星系的位置，发现许多星系集中在图像中央区域。当测量该星系团中所有星系的位置和红移时，得到了如图一所示的分布。

通过这些观测数据，估算该星系团的总质量，并以太阳质量表示。假设该星系团处于动力学平衡状态，其红移分布的均方根弥散为\(\sigma_{z}=\sqrt{\langle(z-0.7)^{2}\rangle}=0.0005\)。在考虑星系的平均速度、质量和空间分布时，可做合理近似。

已知标准宇宙学模型中\(\bar{z}=0.7\)对应的角直径距离为\(D_{A}=1500\) Mpc。忽略距离上的宇宙学效应。

官方解答

根据维里定理： $$U+2K=0$$ 其中\(U\)为总引力势能，\(K\)为总动能。假设所有星系质量为平均质量\(\langle m\rangle=M_{T}/N\)，则： $$K=\frac{1}{2}M_{T}\sigma_{v}^{2}$$ 其中径向速度弥散\(\sigma_{v_r}=c\cdot\sigma_z=1.499\times10^5\ \mathrm{m/s}\)。假设三维速度各向同性，则： $$\sigma_{v}^{2}=3\sigma_{v_r}^{2}$$ 引力势能估算为均匀球体的结合能： $$U=-\frac{3}{5}\frac{GM_T^2}{R}$$ 其中星系团半径： $$R=\frac{D_A\cdot\Delta\theta}{2}=2.3143\times10^{23}\ \mathrm{m}$$ 联立维里定理得： $$M_T = \frac{5R\sigma_{v_r}^2}{G} = \frac{5 \times 2.314 \times 10^{23} \times (1.499 \times 10^5)^2}{6.67 \times 10^{-11}}\ \mathrm{kg}$$ 计算得： $$M_T \approx 2.0 \times 10^{14} M_\odot$$

其他势能估算方法： 1. 通过粒子对势能求和： $$U = -\frac{1}{2}\frac{GM_T^2}{R}$$ 2. 量纲分析： $$U = -\frac{GM_T^2}{R}$$