“2021年IOAA理论第12题-速度矢量图”的版本间的差异
Jingsong Guo(讨论 | 贡献) (创建页面,内容为“==英文题目== ==中文翻译== ==解答==”) |
(→英文题目) |
||
| 第1行: | 第1行: | ||
==英文题目== | ==英文题目== | ||
| + | In curvilinear motion of a planet around a star, the direction of the velocity vector changes continuously. This can be represented by a so-called "trajectory in velocity space" and is obtained as follows: for each point on the spatial trajectory, the corresponding velocity vector is drawn so that its starting point is at the origin of the velocity space, and its magnitude and direction is the same as the velocity vector at that point. The tip of this variable velocity vector generates a curve in velocity space. (The name 'hodograph' was given to this curve by Hamilton in 1846.) | ||
| + | |||
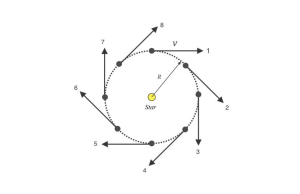
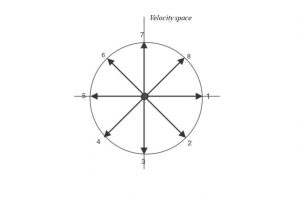
| + | As an example, see figures 1 and 2 below. For a circular orbit (Figure 1), the magnitude of the velocity is constant and therefore, the hodograph (Figure 2) of the velocity vector for Keplerian circular motion is also a circle, the center of which is located at the origin of the velocity space. The radius of this circle is equal to the constant magnitude of the circular velocity. | ||
| + | [[文件:1005135449.png|居中|缩略图|Fig. 1 Spatial trajectory of the Planet with Uniform Circular Motion around the star.]] | ||
| + | [[文件:1005135529.png|居中|缩略图|Fig. 2 Corresponding hodograph]] | ||
| + | 12.1 Write an expression for the radius of the hodograph in Fig. 2, as a function of the mass $$𝑀$$ of the star, and the radius $$𝑅$$ of the circular orbit of the planet's motion.(1.0pt) | ||
| + | |||
| + | 12.2 For a planet in a Keplerian trajectory, write the expression for centripetal acceleration vector $$(\vec{a} )$$ and the magnitude of angular momentum $$(𝐿)$$. For any Keplerian trajectory, it is true that | ||
| + | |||
| + | $$\left | \Delta \upsilon \right | =k\Delta \theta $$ | ||
| + | |||
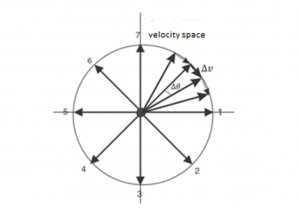
| + | Where $$𝑘$$ is a constant for each type of Keplerian trajectory. Find the expression for the constant $$𝑘$$ as a function of the masses $$𝑀$$ and $$𝑚$$ of the star and the planet, respectively, and the angular momentum, $$𝐿$$.(Eq.1) allows us to conclude that for any Keplerian trajectory, the hodograph $$(\upsilon 𝑎𝑠 𝑎 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 \theta )$$ is a circle, but except for circular motion, the centre of the hodograph does not coincide with the star. It is not necessary to prove this result, you may simply accept it as a given. For the hodograph of uniform circular motion, the compliance with (eq.1) is completely obvious, as evidenced in Fig. 3(4.0pt) | ||
| + | [[文件:1005141716.png|居中|缩略图|Fig. 3]] | ||
| + | 12.3 Determine the expression of the constant $$𝑘$$ for the hodograph of circular planetary motion.(2.0pt) | ||
| + | |||
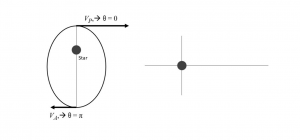
| + | 12.4 Given that the hodograph of the Keplerian elliptical motion is a circle, determine the radius of this hodograph and the distance between the center of the hodograph and the position of the star, as a function of the velocities at periastron and apoastron. Draw a rough sketch of the hodograph in the answer sheet as per the schematic shown in Fig. 4. The black circle is the star.(4.0pt) | ||
| + | [[文件:1005141835.png|居中|缩略图|Fig. 4]] | ||
| + | 12.5 Similarly, for the parabolic Keplerian trajectory, determine the radius of the corresponding hodograph and the distance from the center of that hodograph circle to the star. Express the radius as a function of the velocity at periastron. Draw a rough sketch of the hodograph circle in the answer sheet.(4.0pt) | ||
==中文翻译== | ==中文翻译== | ||
==解答== | ==解答== | ||
2022年10月5日 (三) 14:20的版本
英文题目
In curvilinear motion of a planet around a star, the direction of the velocity vector changes continuously. This can be represented by a so-called "trajectory in velocity space" and is obtained as follows: for each point on the spatial trajectory, the corresponding velocity vector is drawn so that its starting point is at the origin of the velocity space, and its magnitude and direction is the same as the velocity vector at that point. The tip of this variable velocity vector generates a curve in velocity space. (The name 'hodograph' was given to this curve by Hamilton in 1846.)
As an example, see figures 1 and 2 below. For a circular orbit (Figure 1), the magnitude of the velocity is constant and therefore, the hodograph (Figure 2) of the velocity vector for Keplerian circular motion is also a circle, the center of which is located at the origin of the velocity space. The radius of this circle is equal to the constant magnitude of the circular velocity.
12.1 Write an expression for the radius of the hodograph in Fig. 2, as a function of the mass $$𝑀$$ of the star, and the radius $$𝑅$$ of the circular orbit of the planet's motion.(1.0pt)
12.2 For a planet in a Keplerian trajectory, write the expression for centripetal acceleration vector $$(\vec{a} )$$ and the magnitude of angular momentum $$(𝐿)$$. For any Keplerian trajectory, it is true that
$$\left | \Delta \upsilon \right | =k\Delta \theta $$
Where $$𝑘$$ is a constant for each type of Keplerian trajectory. Find the expression for the constant $$𝑘$$ as a function of the masses $$𝑀$$ and $$𝑚$$ of the star and the planet, respectively, and the angular momentum, $$𝐿$$.(Eq.1) allows us to conclude that for any Keplerian trajectory, the hodograph $$(\upsilon 𝑎𝑠 𝑎 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 \theta )$$ is a circle, but except for circular motion, the centre of the hodograph does not coincide with the star. It is not necessary to prove this result, you may simply accept it as a given. For the hodograph of uniform circular motion, the compliance with (eq.1) is completely obvious, as evidenced in Fig. 3(4.0pt)
12.3 Determine the expression of the constant $$𝑘$$ for the hodograph of circular planetary motion.(2.0pt)
12.4 Given that the hodograph of the Keplerian elliptical motion is a circle, determine the radius of this hodograph and the distance between the center of the hodograph and the position of the star, as a function of the velocities at periastron and apoastron. Draw a rough sketch of the hodograph in the answer sheet as per the schematic shown in Fig. 4. The black circle is the star.(4.0pt)
12.5 Similarly, for the parabolic Keplerian trajectory, determine the radius of the corresponding hodograph and the distance from the center of that hodograph circle to the star. Express the radius as a function of the velocity at periastron. Draw a rough sketch of the hodograph circle in the answer sheet.(4.0pt)