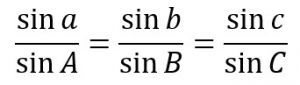天体视运动
|
|
目录
知识点
一、球面几何基础
1. 大圆、小圆
球面被经过球心的平面所截得的圆叫做大圆。被不经过球心的平面所截得的圆叫做小圆。
2.球面上的距离
大圆上两点之间劣弧的长度叫做球面上两点间的距离。
D=r×θ
D为球面距离,r为半径,θ为角距。θ极小r极大时,这也是两点直线距离的公式
3. 球面三角形
三条大圆的劣弧首尾顺次相接构成的封闭图形成为球面三角形。三条劣弧称为球面三角形的边。用边的字母表示弧长或弧所对应球心角的大小,用角的字母表示两夹边所对应两大圆面的二面角。 从球心出发,过球面三角形三个顶点作射线,三条射线之间构成三个平面。这样的图形称为三面角。三面角O-ABC中,两个面角之和大于第三个面角。(∠AOB+∠COB >∠AOC)
性质1:两边之和大于第三边,两边之差小于第三边。
性质2:等角对等边,大角对大边。
性质3:球面三角形的周长小于大圆周长。
性质4:球面三角形的内角和大于π小于2π。其面积的计算公式是:
S=(E-π)×r^2
E为内角和,r为球半径。
====== 4. 球面三角形的边角关系 ======
(1)球面正弦定理
文字表述:球面三角各边的正弦与其对角的正弦成比例
(2)球面余弦定理
阿拉伯数学家巴塔尼(al-Battani)使用几何法证明
文字表述:球面三角边的余弦等于其他两边余弦之积加上两边正弦及其夹角余弦之乘积
cos𝑎= cos 𝑏∙𝑐𝑜𝑠 𝑐+sin𝑏∙sin𝑐∙cos𝐴
也有角的余弦定理
cos𝐴=−cos 𝐵∙cos𝐶+sin𝐵∙sin𝐶∙cos𝑎
(3)球面五元素公式(不用记!!!)
可以使用余弦定理推出,了解即可
sinA cosb=cosB sinC+sinB cosC cosa
sinA cosc=cosC sinB+sinC cosB cosa
sina cosB=cosb sinc-sinb cosc cosA
sina cosC=cosc sinb-sinc cosb cosA
(4)球面四元素公式(不用记!!!)
cotA sinC=-cosCcosb+sinb cota
cotA sinB=-cosB cosc+sinc cota
二、天球坐标系
1. 天球的概念
天球是一个与地球同球心,并有相同的自转轴,半径无限大的球。其目的是将天体沿观测者视线投影到球面上,以便于研究天体及其相对位置。有时还将天球球心设置在某些特殊点,如地心和日心,相应的天球分别称为地心天球和日心天球。
天球之基本定义如下
(1)天球半径为无限大,也可以任意值替代。
(2)使用天球中心到天体在天球上的投影点表示其位置。
(3)天球之中心可选,由地心、日心、站心等。
(4)天球上任意两点之大圆弧大小为其距离
2. 天球坐标系
意义:确定天体在天球上的位置
三要素:基本轴、基本点、坐标范围和量度方向。
3. 几个基本的球面坐标系
(1)地理经纬度:地理纬度φ、地理经度λ
基本轴:地球自转轴
基本点:格林尼治天文台G。坐标西正东负、北正南负。
海里:沿经度圈,纬度每变化1”的球面距离。
(2)地平坐标系:地平高度h或天顶距z、方位角A
基本轴:铅直线
地平高度 h (Altitude)
天顶距 z=90°-h (Zenith Distance)
方位角 A (Azimuth)
(A自北点起算,顺时针计,向西为正)
也有部分老教材自南点起算,请注意阅读题目要求再作答
(3)赤道坐标系:赤经(R.A.)α或时角t、赤纬(Dec.)δ
赤纬 Dec. δ
赤经 R.A. α
时角 Hour Angle H或t
时角由主点(Q)起算,沿视运动方向为正(西正)
赤经由春分点(♈︎)起算,沿时角的反方向为正(东正)
(4)黄道坐标系
黄纬 Ecliptic latitude β
黄经 Ecliptic longitude λ
黄经由春分点(♈︎)起算,与赤经正方向一致(东正)
黄道坐标系可以比照赤道坐标系理解
4. 四季星空
1928年,国际天文学联合会将各种星座标准化,订立了88个大多来自古希腊传统和欧洲航海家命名的标准星座。其中最出名者当属黄道12星座。
黄道十二宫是黄道带上人为划分(与实际星座位置不一致)的均等区域,以数学方式的划分为十二个30°的扇区。
例:太阳在那个星座待的时间最短?在那个黄道宫待的时间最短?
答案:天蝎座、人马宫
5. 黄道十二宫
白羊宫(Aries, ♈︎);金牛宫(Taurus, ♉︎);双子宫(Gemini, ♊︎);巨蟹宫(Cancer, ♋︎);
狮子宫(Leo, ♌︎);处女宫(Virgo, ♍︎);天秤宫(Libra, ♎︎);天蝎宫(Scorpio, ♏︎);
人马宫(Sagittarius, ♐︎);摩羯宫(Capricornus, ♑︎);宝瓶宫(Aquarius, ♒︎);双鱼宫(Pisces, ♓︎)。
三、天体的视运动
1. 周日视运动
本质是地球的自转,会显示出星轨(周日圈)。一切恒星均绕着北天极(近似为北极星所在位置)匀速旋转。
其周期与地球自转周期相等,为24恒星时,即23h56m太阳时 所以1小时大约转15°,转1°需要4min。
在不同纬度观测之周日视运动不同:
(1)北极和南极:所有天体沿水平小圆运动
(2)赤道:所有天体东升西落
(3)北半球中纬度处:北极星高度等于当地地理纬度,所有天体绕极轴转动。(可以利用左手螺旋定则判断周日视运动方向)
h_Polaris=90⁰-φ
(4)南半球中纬度处,画图推算即可
2. 天体中天
子午圈:通过天极和天顶的大圆。 天体通过子午圈称为中天。离天顶近的称为上中天,反之则称为下中天。在北半球,上、下中天有如下关系:
h_max=90⁰-|δ-φ|
h_min=-90⁰+|δ+φ|
h_max+h_min=2×δ
在天顶以北上中天时,δ-φ>0。在天顶以南,则δ-φ<0
3. 永不升和永不落(拱极星)天体
由于所有天体绕极轴转动,所以在特定纬度,部分星体永不落或永不升。在北半球,满足如下关系:
永不落:𝛿>90°−𝜙
永不升:𝛿<−(90°−𝜙)
地理位置越靠近两极恒显/隐星区(即恒显隐圈)越大
在赤道,没有天体永不升、落
4. 月相
恒星月:月球绕地球公转的周期。
朔望月:月相变化的周期,长于恒星月。
决定因素:日月角距的变化,每天13.2⁰。自朔到望。
5. 日月食
月食:只能在望日发生,只能在月食限内发生,一年两食季。
日食:只能在朔日发生,只能在日食限内发生,一年两食季。
食分:月球视直径被地球本影遮挡住部分与地球视直径之比。日偏食的食分是太阳视圆面直径被遮挡住部分与剩余部分之比。
月亮运动自西向东,速度约1km/s
题目
例1:设地球的半径为6400km,在北纬30。的纬线上有A、B两点。若O为北纬30。圈所成小圆的圆心,∠AOB=90。,那么AB两点间球面距离为多少?
例2:地球上两城市A, B的坐标分别为(φ1,λ1)和(φ2,λ2)。若地球半径为R,求出两城市间实际球面距离。
例3:全天约有6000颗可见恒星,假设他们均匀分布。若某地纬度是北纬30⁰,那么在该地的观测者可以观测到大约多少颗永不落天体?
球面几何练习题
练习1:设地球赤道上两城市A、B,地理经度分别为东经15。和西经30。。求两地之间的球面距离。(地球半径为6400km)
练习2:
(1)证明球面三角形性质3。
(2)利用几何法、向量法证明球面三角余弦定理。
练习3:半径为10的球面上有一个边长为2、4/3、3的球面三角形。求该球面三角形的内角。
题目来源
CNAO 预赛决赛题
人教版《高中数学选修3-3 球面上的几何》
《球面天文学与天体力学基础》(肖锋 编)